T(n)=27T(n/3)+(n^3)log(n)的时间复杂度计算
 社区干货
社区干货
2022技术盘点之平台云原生架构演进之道|社区征文
云运营各角色的工作复杂度,提升管理效率和资源交付效率,最终帮助企业降低云上成本,提升人员效率,加速企业的数字化转型。## 二 高可用架构云的时代需要新的技术架构,来帮助企业应用能够更好地利用云计算优势,充... 下图为SmartOps架构全景: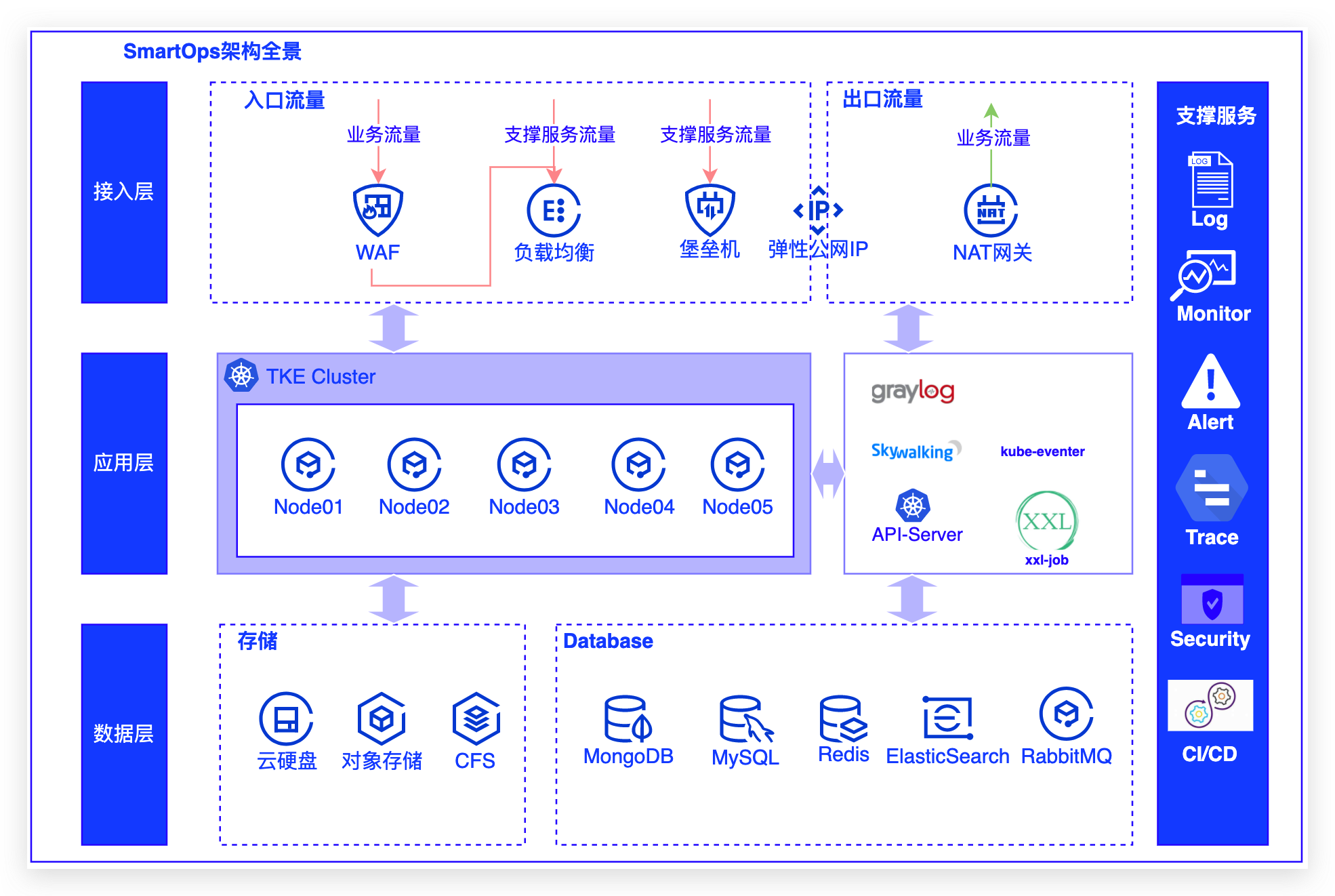- 接入层:通过WAF/SLB,配合NAT网关治理出方向流量,部署有堡垒机进行运维等其他辅助...
万字长文带你漫游数据结构世界|社区征文
同样是`z1 =3.0 - 2.3i `,先找到下一个是 `100`,是一个地址,根据地址找到真实的数据`-2.3i`:## 位(bit)在计算机中表示... [](https://markdownpicture.oss-cn-qingdao.aliyuncs.com/blog/20220108120726.png)但是如此,还是没有彻底解决问题,因为链表很长的情况,只能通过前后两部分查找。不如回到原则:`空间和时间,我们选择时间,那就要...
超复杂调用网下的服务治理新思路
面对这样的复杂度,有三个问题最为突出:**一是难以做容量预估**。微服务已经达到了一定的复杂度,它们的调用关系是非常复杂的:一个核心服务的依赖链可能就有几百个,对每个依赖方做调研或去细致地跟进每个限流策略... 那么该流量触达下游服务时仍应携带标记 TIM1;如果流量来自西瓜视频且携带了 TIM2,那么由这个请求触发下一个在线请求时,它也一定要携带这个 TIM2。这使得整个调用链可以完成串联,类似 Log ID、Trace ID。所以这个...
AI赋能安全技术总结与展望| 社区征文
从而大大减少了分析师的工作时间。在人工智能赋能安全蓬勃发展浪潮中,机器学习技术(包括深度学习技术)在应对网络空间威胁方面起着至关重要的作用。 为了帮助初学者少走弯路以及更多人了解AI赋能安全,笔者总结... 本论文提出了四大类特征:PE section对应的大小(虚拟大小、原始大小、两者比例)、PE section中不同权限section的大小(可读、可写、可执行段对应的虚拟大小之和、原始大小之和、两者比例)、内容复杂度(PE和ASM文件原...
 特惠活动
特惠活动
 T(n)=27T(n/3)+(n^3)log(n)的时间复杂度计算
-优选内容
T(n)=27T(n/3)+(n^3)log(n)的时间复杂度计算
-优选内容
 T(n)=27T(n/3)+(n^3)log(n)的时间复杂度计算
-相关内容
T(n)=27T(n/3)+(n^3)log(n)的时间复杂度计算
-相关内容
干货|湖仓一体架构在火山引擎LAS的探索与实践
 火山引擎湖仓一体分析服务LAS(Lakehouse Analytics Service),是面向湖仓一体架构的 Serverless 数据处理分析服务,提供字节跳动最��
分布式数据库TiDB的设计和架构
 第十二期技术夜校分享嘉宾是DBA大咖——Xiaoyu 他拥有10年+互联网数据库运维经验、在游戏、电商、OTA行业从事过DBA运维工作、在大规�
漫谈开源许可证:开发者需要知道的法理和事例
 来源|字节跳动 Web Infra - Web Solutions 团队 感谢字节跳动开源法务 @孙振华 提供的专业指导和修改意见。 本文仅供开发�
字节跳动数据库的过去、现状与未来
点击上方👆蓝字关注我们!  数据库技术一直是信息技术中极其重要的一环,在步入云原生时代后,云基础
Java SDK
Java SDK,用来简化服务端埋点的复杂度。通过使用SDK,您可以仅仅关注埋点方案而不需要关注具体的上报细节。 1. 使用方法 1.1 SDK 集成如果您需要使用Java SDK,首先需要在pom文件中引入对应的jar: xml
Java SDK
Java SDK,用来简化服务端埋点的复杂度。通过使用SDK,您可以仅仅关注埋点方案而不需要关注具体的上报细节。 1. 使用方法 1.1 SDK 集成如果您需要使用Java SDK,首先需要在pom文件中引入对应的jar: xml
湖仓一体架构在 LAS 服务的探索与实践
火山引擎湖仓一体分析服务 LAS(Lakehouse Analytics Service),是面向湖仓一体架构的 Serverless 数据处理分析服务,提供字节跳动最佳实践的一站式 EB 级海量数据存储计算和交互分析能力,兼容 Spark、Presto 生态,帮助企业轻松构建智能实时湖仓。 LAS 服务是什么?LAS 有哪些优化特性?本文将从基础概念、数
Enhancer-轻量化的字节码增强组件包|得物技术
 **目录** 一、问题描述 二、方案选型 三、技术方案 1. 项目结构 2. 核心组件 3. 增强�
在线学习FTRL介绍及基于Flink实现在线学习流程|社区征文
# 背景 目前互联网已经进入了AI驱动业务发展的阶段,传统的机器学习开发流程基本是以下步骤: 数据收集->特征工程->训练模型->评估模型效果->保存模型,并在线上使用训练的有效模型进行预测。 这种方式主要存在两个瓶颈:模型更新周期慢,不能有效反映线上的变化,最快小时级别,一般是天级�
