q*q.adjoint()是什么意思?
 社区干货
社区干货
供应链库存幂等实战分享
先来了解下什么是幂等。 引自百度百科:幂等(idempotent、idempotence)是一个数学与计算机学概念,常见于抽象代数中。**在编程中一个幂等操作的特点是其任意多次执行所产生的影响均与一次执行的影响相同。** from table_name where month= 9 and product_name =‘中原财富1号’`业务人员一般不具有SQL编程能力,而对于上述这些语句比较简单,但问题发散的场景,业务人员想要查询相应的结果需要找到数据工程人员完成相关流程。流程比较繁琐,而通过nl2sql技术,则可直接将问题转换成相对应的SQL语句用...
VisActor——面向叙事的智能可视化解决方案
点击上方👆蓝字关注我们! VisActor是什么  特惠活动
特惠活动
 q*q.adjoint()是什么意思?
-优选内容
q*q.adjoint()是什么意思?
-优选内容
 q*q.adjoint()是什么意思?
-相关内容
q*q.adjoint()是什么意思?
-相关内容
配置Linux实例NTP服务(Ubuntu 18)
确认是否修改成功。 启动标准NTP服务连接Linux实例,操作详情可查看登录Linux实例。 执行sudo systemctl restart ntp命令,启动NTP服务。 执行systemctl enable ntp命令,设置开机自启动NTP服务。 执行sudo systemctl status ntp命令,查看NTP服务运行状态。 执行命令ntpq -p可查看NTP服务对等端的列表信息(可选)。 配置自定义NTP服务连接Linux实例,操作详情可查看登录Linux实例。 执行sudo vim /etc/ntp.conf命令,打开并编辑...
火山引擎 Redis 云原生实践
Redis 协议是二进制安全的文本协议。它很简单,可以通过 telnet 连接到一个 Redis server 实例上执行 get 和 set 操作。## K8s 简介K8s 是一个容器编排系统,可以自动化容器应用的部署、扩展和管理。K8s 提供了一些基础特性:- **自动装箱**:可指定 K8s 里 Pod 所需资源的最小值和最大值,即 limit 和 request 的值。K8s 可以根据 request 的值做 Pod 调度,在一个节点上拉起 Pod。- **服务发现与负载均衡**:K8s 提供基...
社区征文|ChatGPT教我如何面试
###### Q:Python的GIL锁是什么?GIL锁(Global Interpreter Lock)是指在Python解释器中存在的一种机制,它限制了同一时刻只有一个线程能够执行Python字节码。因此,即使是多核处理器,Python程序在执行时也只能使用一... 这个工厂对象通过使用一个与创建对象相关的算法来决定应该创建哪种对象。例如,一个简单的工厂模式可能用来创建不同类型的按钮,如果要创建一个新的按钮,只需要给工厂对象传入一个参数来指定要创建哪种类型的按钮。...
模型效果FAQ
Q:语音识别的准确率是如何衡量的,目前火山引擎的准确率大概是在什么水平?A:语音识别的准确率用字/词错误率(Char / Word Error Rate,CER / WER)来衡量,准确率 = 1 - 字错率。目前火山引擎的语音识别,在大部分的场景可以达到 85%~95% 的准确率。 Q:如何测试我的业务场景的识别准确率?A:您可以标注真实场景的测试音频(最好 > 3h),根据标注结果和识别结果计算 CER / WER;您也可以提供音频给我们,由我们进行标注和测试(将额外收取费用...
Linux操作系统挂载多个数据盘如何做软raid
align-check optimal 1 //查看分区是否对齐paint //查看分区表q //退出parted工具partprobe //系统重读分区表fdisk -lu /dev/cdb //查看新分区信息````出现如下回显,则表明操作成功: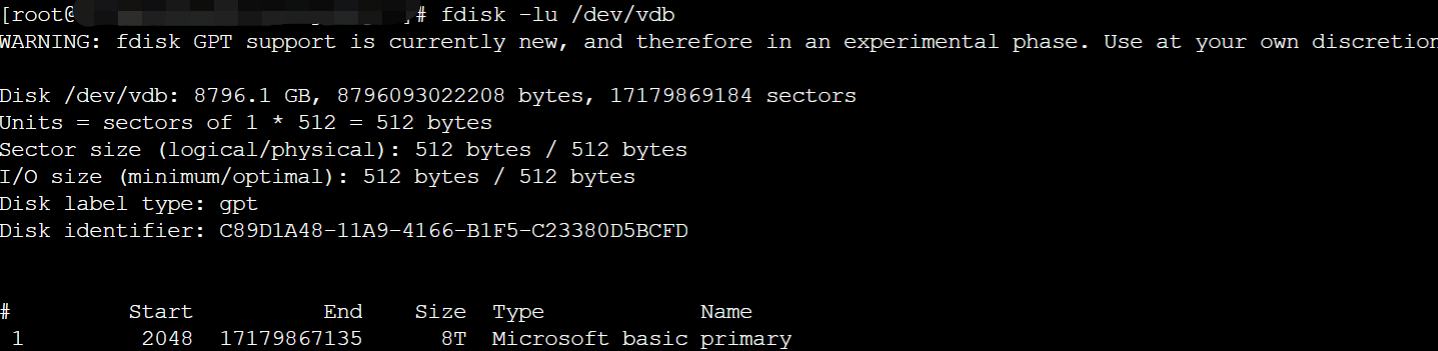> 其余新挂载磁盘的分区方式与本方式相同。3. 依次执行以下命令创建软RAID````undefinedyum install madam //安...
使用内存泄漏监控和泄漏兜底服务
q)包装Activity,在Activity被垃圾回收器回收后,reference会被放入内部的ReferenceQueue中。也就是说,从队列ReferenceQueue取出来的所有reference,它们指向的真实对象都已经成功被回收了。 什么是内存泄漏兜底? 一些泄漏的对象的生命周期已经结束,但依然存在着强引用,导致对象没有办法被GC回收。通过代码主动断开泄露对象到GC ROOT的链路,或者释放掉泄露对象的引用对象,让这些泄露对象在下次GC时候可以被回收掉,释放出内存空间,...
从应用看火山引擎 AB 测试 (DataTester) 的最佳实践
**A/B 测试到底能做什么?有哪些业务场景?**  大家可以从上图中的数字感受到在字节跳动 A/B 实验应用的广度和深度,并且这些数字还在继续快速上涨。A/B 实验在临床医学和生物制药...
API调用指南
目前支持system/user/assistant content:消息内容 消息是列表形式,依次记录了消息聊天上下文(第一个是最早的对话,最后一个是最新的对话)。以 Q 表示 user 消息, A 表示 assistant,不考虑 system 消息,输入形式如:Q1, A1, Q2, A2, Q3(输入应该是奇数个,为若干个 Q/A 对后面一个单独的 Q),system 消息可以按需插入其中。 目前content支持传入2种类型: string与list(object) a. "type": "image_url"用于传入图片信息 i. image_url...
图谱构建的基石: 实体关系抽取总结与实践|社区征文
=&rk3s=8031ce6d&x-expires=1713975672&x-signature=AxXGxFRA4RqXXkxTtLnnKC3x6Fg%3D)1. Entity Model 1. 首先输入句子到预训练Encoder(如BERT)中去,任一token $$x_{t}$$ 得到上下文表征 $$X_{t}$$ 2. 计算span representation: $$\mathbf{h}_{e}\left(s_{i}\right)=\left[\mathbf{x}_{S T A R T(i)} ; \mathbf{x}_{E N D(i)} ; \phi\left(s_{i}\right)\right]$$ 3. 将span representation输入到两层FFN去生成实...
