指标归因功能是用于探索多个相关指标对核心指标变动的影响，包括乘法因子的贡献和非乘法公式关系中各因子的贡献。根据用户配置，系统会每天/每周自动对相关指标对核心指标的影响程度进行分析。（归因决策为增值模块，需单独付费方可使用，自V2.62.0及以上版本支持。如您需要使用，请联系贵公司的商务人员或客户成功经理咨询购买事宜）。

乘法指标拆解归因： 乘法因子贡献同时也适用于除法指标，只需要为分母建立一个倒数字段即可。
乘法指标拆解的适用场景：核心指标可由多个相关指标通过乘法计算得到，比如 GMV=访问量转化率客单价。
非乘法指标拆解归因： 在实际业务中核心指标会由由多个指标复杂的四则运算得到，或者没有公式关系但存在相关性，此时也需要量化评估子指标对核心指标变化的贡献。

2.1 创建配置

第一步：进入归因报告模块，在「我创建的」标签页内，点击「新建」按钮。

第二步：在弹出的归因配置抽屉页输入归因配置名称，还可添加归因报告说明。选择归因类型为指标归因。

2.2 配置核心指标

2.2.1 选择指标

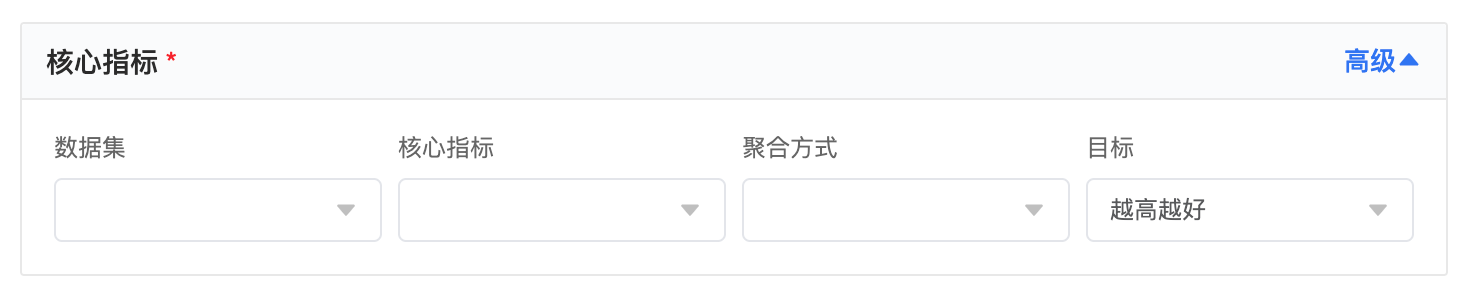
您需要配置以下内容：
（1）数据集： 从下拉列表中选择一个数据集。下拉列表中的选项为当前项目内具有读权限及以上权限的所有数据集。
（2）核心指标： 从下拉列表中选择一个指标
（3）聚合方式： 当选择完指标后，需要制定该指标的聚合方式。如果是已聚合过的指标，例如表达式为sum([新增用户数])，那么此处自动选为“聚合”且不可编辑。
（4）目标：

• 选项内容：越高越好 或 越低越好
• 作用层面：报告的显示层面
• 应用范围：上升下降 Icon 的颜色

2.2.2 指定业务日期

您需要指定以下内容：
（1）业务日期字段： 以哪个日期字段作为核心指标的统计口径。
（2）计算粒度： 可按日、周、双周、月、双月 聚合。其中周、双周可以自定义开始日和结束日。

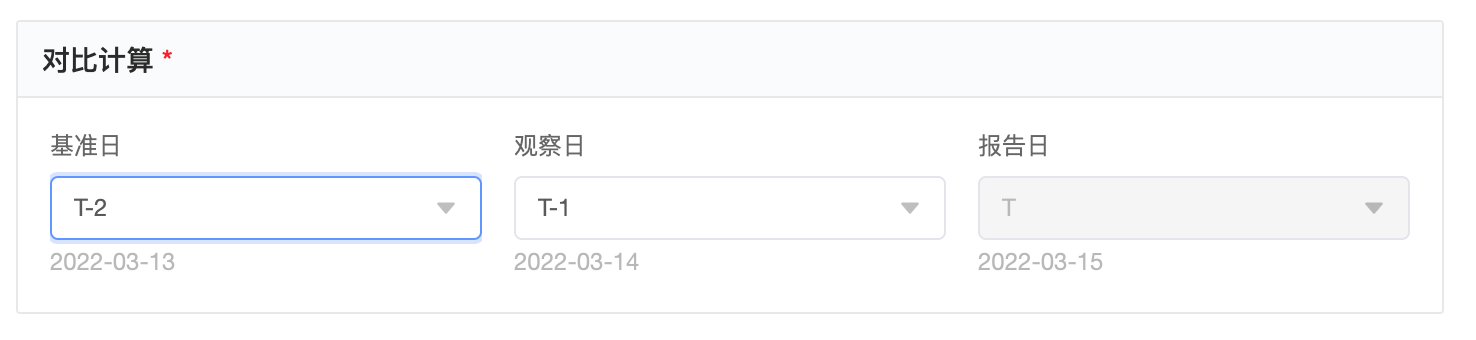
2.2.3 指定对比计算日期

• 天粒度： 昨天对比前天的变化值进行归因。那么基准日为T-2，观察日为T-1，报告日为T
• 周粒度： 上周对比上上周的变化值进行归因，在每周一计算运行归因报告。那么基准日为W-2，观察日为W-1，报告日为周一 。

2.2.4 筛选条件（选填）

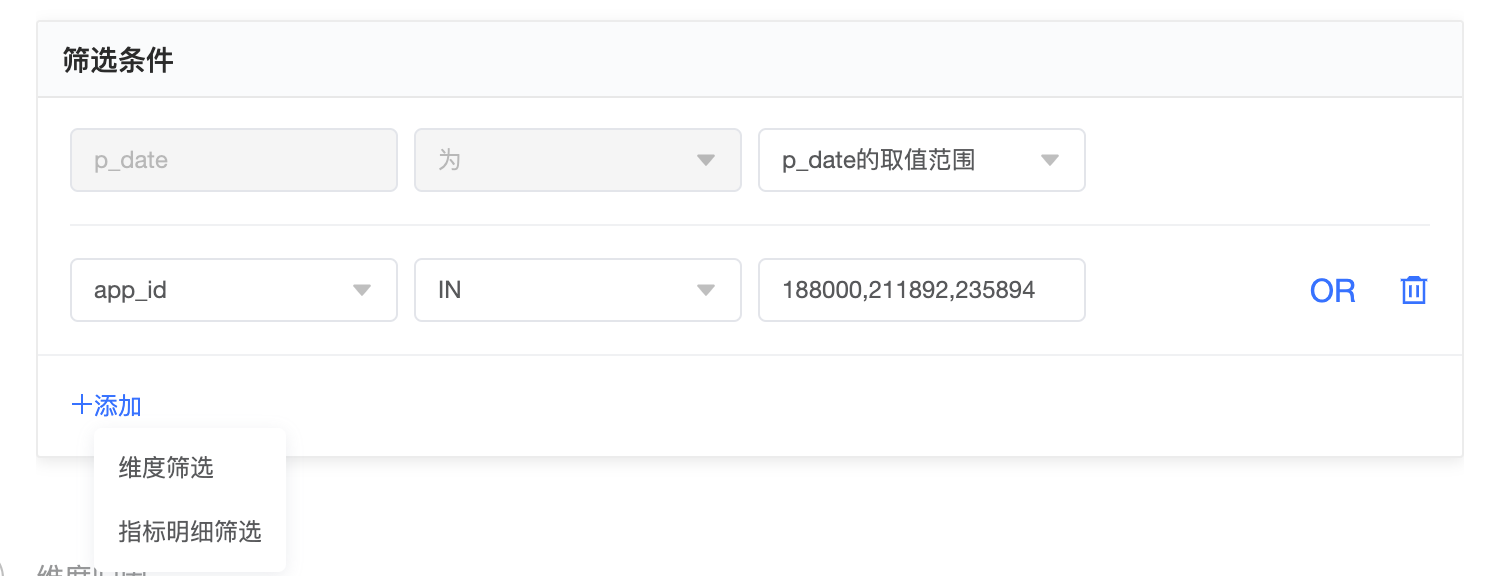
每个归因配置都必须指定分区日期（p_date）的范围。

• 全量表的特征： 在可视化查询页面里p_date选最近有数一天且不用改动。
• 增量表的特征： 在可视化查询页面里p_date通常需要选最近XX天等范围，随着观测日期范围的变化而变化。

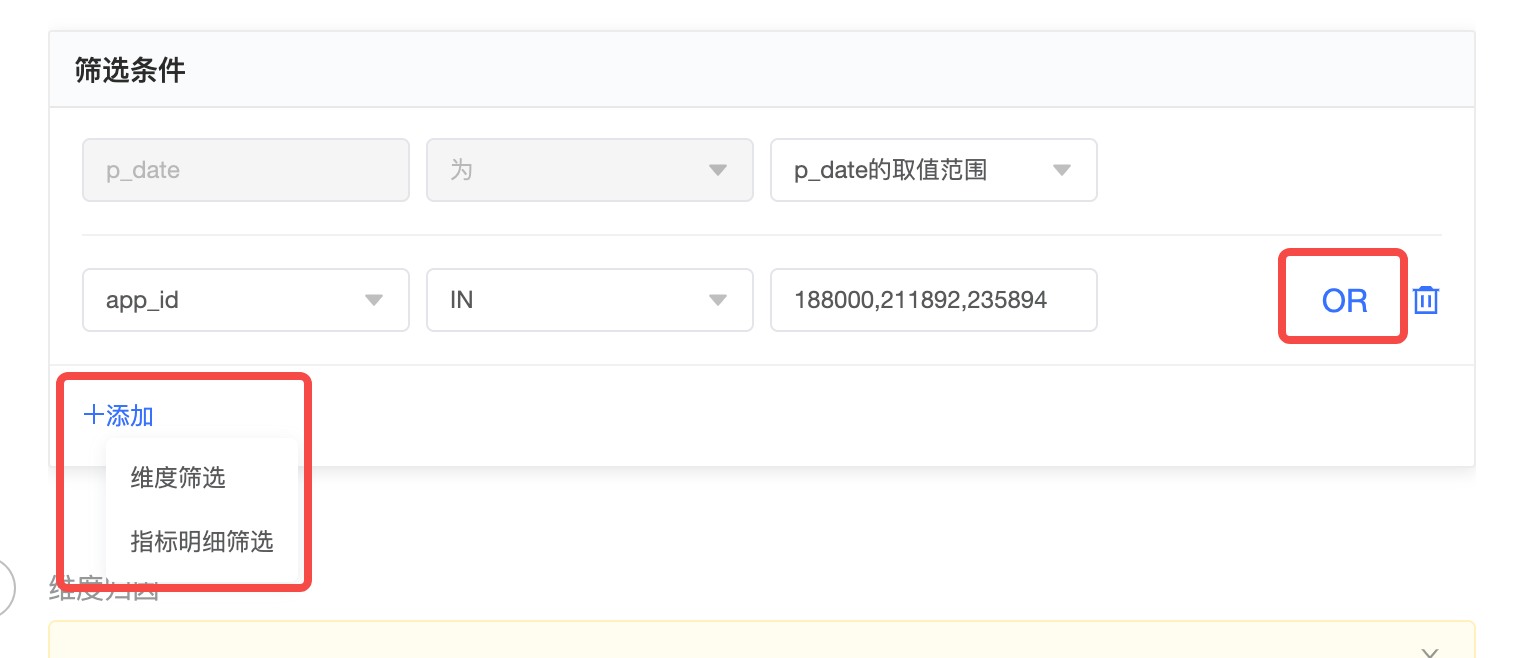
左下角的添加按钮表示添加一个 AND 条件，右上角的 OR 按钮表示在当前条件后添加一个 OR 条件。
每组 OR 条件之外是用 AND 条件连接。例如：（省份=河北 OR 地区=华南）AND （性别=男）。

2.2.5 创建网页

在「新增归因」中，您可以直接输入以http://或https://开头的链接地址即可创建网页。

若需对网页执行重命名、复制及删除操作，请点击“更多”，将为您展开相关内容。

2.3 配置指标归因

2.3.1 乘法指标

当前指标归因支持将核心指标拆解为多个乘法因子相乘的等式，探索每个乘法因子对核心指标变动的贡献率。
需要将核心指标的相关乘法因子指标指定，且需保证它们相乘等于核心指标。

2.3.2 非乘法指标

首先，您需要添加至少2个用于进行归因的过程性指标，这些指标可以和核心指标来自不同的数据集。

其次，您需要指定下图所展示的内容：

最后，针对每个过程指标模块，需要指定过程指标名称。
注意：

• 同一份报告中指标名称不可重复，否则无法保存配置。
• 可以操作每个核心指标模块右上角的复制、删除 按钮进行快速操作。

2.4 设置分组维度

分组维度的作用类似于仪表盘中的公共筛选器，支持基于每个分组维度项的筛选条件下去计算生成一个归因报告。在归因报告中放在顶部，以平铺的形式显示。

注意： 分组维度支持添加多个，但是多个分组维度之间是 or 的关系，并不是 and 关系，所以建议只添加1个分组维度。

2.5 核心指标异动

用户可以通过在维度归因报告中查看核心指标是否异动，来增加辅助业务决策的信息。
勾选“显示”后，需要继续指定异动检测方法，可选算法或自定义规则，功能和异动分析报告配置十分类似。

对应在归因报告和推送卡片的头部将显示核心指标异动的结果：

• 推送卡片

• 归因报告

3.1 乘法指标归因的报告

报告的表格显示了所有乘法因子的贡献值和贡献率，以及其自身的变化。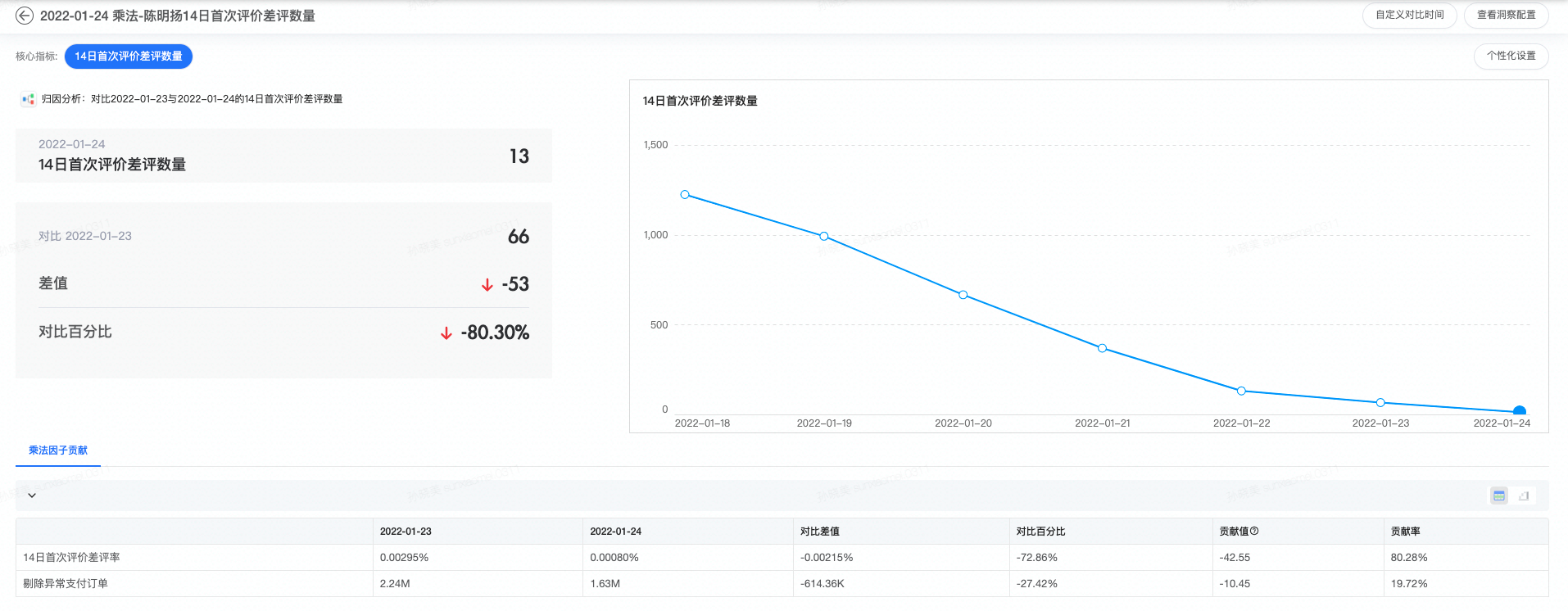

3.2 非乘法指标归因的报告

报告的表格显示参与计算的过程指标对核心指标变化的贡献情况。

4.1 乘法指标归因算法

算法详细介绍：指标归因-算法

4.2 非乘法指标归因算法

首先采用 XGBoost算法 计算过程指标的重要性（与核心指标相关性）。
然后对重要性高的过程指标 采用 Shapley值法 进行贡献值计算，从而得出对核心指标变化值的量化解释。
算法详细介绍：指标归因-算法